Developers Summit 2023 Summer でサーバーレスについて話してきました
こんにちは、チェシャ猫です。
先日開催された Developers Summit 2023 Summer で、サーバーレスコンピューティングの形式化について登壇してきました。公募 CFP 枠です。
内容は Jangda et al. (2019) による論文 "Formal Foundations of Serverless Computing" を軸にしています。この論文はサーバーレスコンピューティングに対して操作的意味論の定式化を行うものであり、プログラミングの国際学会 OOPSLA '19 の Distinguished Paper を受賞しています。
なお、同様のテーマは AWS Dev Day 2022 でも登壇しています。スライドも大部分は共通ですが、解説が不足していた点を具体的に補足したり、逆に意図して細部を省略したりしてあるため、前回から比べると全体としてはかなりわかりやすくなっているはずです。
Twitter やチャットでの反響は正直なところいまひとつでしたが、スライドの解説資料としての出来には満足しています。
最後にセッションの本筋とは直接関係しない余談を一つ。質疑応答の最後、自分が登壇する時に何を重要だと思っているかについて触れる機会がありました。自分の中では以前から考えていたことですが、今まで登壇という場で述べる機会がなかったので今回話せて良かったです。ちなみに何を話したのかは、当日の講演を聞いた人だけの秘密。
2022 年、アウトプットの思い出
こんにちは、チェシャ猫です。2022 年中は大変お世話になりました。本記事では自分自身への備忘も兼ねて、本年度の対外的な発表についてまとめておこうと思います。
2022 年の活動実績
2022 年の登壇は 3 件でした。うち(先着や抽選ではなく)CFP に応募して採択されたものは 2 件です。以前は頻繁に登壇していた LT の回数を今年はかなり控えていたこともあり、件数としては少ない水準となりました。
賢く「振り分ける」ための Topology Aware Hints
Kubernetes Meetup Tokyo #52 での発表です。
Kubernetes の Service に対するトラフィックを、ネットワーク的に近い Pod に対してルーティングする機能、Topology Aware Hints を解説しています。具体的には Node に対する Label で表現された各 Zone に対して、その Zone に存在する Node の CPU 数の比によってトラフィックのルーティング先が決まります。ルーティングのロジックはやや複雑ですが、もし興味があればスライドを参照してください。
ちなみに、Kubernetes においてネットワークトポロジに応じてトラフィックを操作する仕組みは、今回の Topology Aware Hints 以前にも、いくつかの KEP で提案され没になっています。スライド中では過去の提案がどのような問題意識でなされ、なぜ没になったのか、その辺りの経緯も解説してみました。
サーバーレスは操作的意味論の夢を見るか?
AWS Dev Day Japan 2022 での発表です。公募 CPF 枠で、昨年も登壇しているので 2 年連続の採択になります。
内容としては、サーバレスコンピューティングに対して操作的意味論による基礎づけを行なった 2019 年の Jangda らの論文、Formal foundations of serverless computing について解説しました。OOPSLA '19 の Distinguished Paper にも選出されています。
解説したのはこの論文のうち前半部分、具体的には Section 4 まで相当です。イベントの参加者の大半はこのような形式化には慣れていないことを考え、後半部分のより現実的かつ複雑な意味論を諦める代わりに「操作的意味論とはなにか」「推論規則の読み方」「双模倣の例」といった基本的な事項を解説することを選択しました。もし興味があれば元論文にもチャレンジしてみてください。
また、同じ論文について Qiita に記事を書かれている方も発見しました。こちらの記事は操作的意味論への基本的な知識は仮定されている一方、元論文の前半だけでなく最後のセクションまで満遍なく記事として起こされています。
謎は全て解けた!安楽椅子探偵に捧げる AWS ネットワーク分析入門
CloudNatice Days Tokyo 2022 での発表です。公募 CFP 枠です。
内容は AWS においてネットワークに関するクエリに回答するエンジン Tiros にまつわるものです。Tiros は内部的に SMT ソルバの一種 MonoSAT を使用しており、AWS のネットワーク構造をグラフ構造としてエンコードして MonoSAT に解かせることで、コンポーネント間の到達可能性について推論を行います。
内容としては昨年の AWS Dev Day Online Japan と共通する部分が多いですが、中盤の SMT ソルバに関する一般論と SAT 問題の単調性に関する解説を一部削り、その代わりに前回扱えなかった Blocked Path Analysis の解説を追加してあります。Blocked Path Analysis は SMT ソルバを使用する Tiros の大きな特徴であり、普通にイメージする Packet Probing によるネットワーク検査と比べて明確な挙動の差が生じる部分です。今回 Blocked Path Analysis について解説を追加できたことで、前回のスライドと比較してもより有意義な解説になったと思います。
まとめ
以上、2022 年のスライド一覧とセルフ短評でした。
ところで、Speaker Deck のスライドページをご覧いただくと分かる通り、今年の登壇はスライド閲覧数が異様に少ないのも特徴です。特に CloudNative Days Tokyo 2022 のスライド は、大規模イベントかつ Twitter 上でそれなりに Like されているにもかかわらず、スライド閲覧数が以前の LT の水準にすら達していません。
もともと Speaker Deck の閲覧数は「たまたま界隈の有名人が好意的なコメントをくれた」「はてなブックマークで初動が良かった」といった要素で変動するため、所詮は水物であり、過剰に意識してもいいことはありません。とはいえモチベーションに影響するのも事実なので、現状の登壇 + スライド公開という発表手段を来年以降もメインに据えるかどうかも含め、ちょっと検討しようかなと考えています。情報のストックと検索性という意味では、スライドよりもブログ記事の方が望ましいかもしれませんね。去年も同じことを書いてますが…。
それでは、2023 年も張り切っていきましょう。よろしくお願いいたします。
CloudNative Days Tokyo 2022 に「謎は全て解けた! 安楽椅子探偵に捧げる AWS ネットワーク分析入門」というタイトルで登壇してきました
こんにちは、チェシャ猫です。
先日開催された CloudNative Days Tokyo 2022 で、SMT ソルバを用いた AWS のネットワーク検査機能、VPC Rechability Analyzer と VPC Network Access Analyzer について話してきました。公募 CFP 枠です。
イベントサイトにて録画も視聴可能です。
今回の登壇は「事前録画を提出」「当日リモートで登壇」「現地で登壇」のいずれの方式が選択可能だったのですが、自分は現地で登壇しました。
現地参加者全員が一つの部屋に集まる Keynote では意外と人がいるなという印象でしたが、午後のブレイクアウトセッションでは 6 部屋あったこともあり、自分のセッションの現地参加者は 10 数人程度でした。
完全オフラインだった頃の熱気には及びませんが、対面でお話しする場は数年ぶりで、聴衆の反応を見ながらプレゼンできる体験はやはり良いものです。
講演概要
ネットワークのトラブルシューティングは辛い作業になりがちです。特に AWS の VPC ネットワークは多数の設定が必要であり、疎通ができない場合にその原因を発見・修正するためには往々にして高いスキルが必要となります。
このような状況に対処し、誰でも体系的にネットワーク不通の原因を解消できる助けにするため、AWS は VPC Reachability Analyzer と VPC Network Access Anazlyer という二つの機能を提供しています。前者は、プロトコルやポート番号を指定することで二つのコンポーネント間の疎通を確認し、到達可能でない場合はその原因となっているコンポーネントを指摘します。また後者は、あらかじめクエリを登録しておくことで条件に合致する経路を一覧表示・分析し、コンプライアンス準拠等の目的に役立てることができます。
この機能には「到達不可能な場合であっても、その原因部分を含め送信元から送信先への完全な経路が得られる」という特徴があります。一般によく用いられるパケットを送出するタイプの疎通確認 (Packet Probing) において、不通となっているコンポーネントから先の経路情報は得られません。すなわち、VPC Rechability Analyzer はパケット送出によって経路を探索しているわけではない、ということがわかります。
今回の講演ではこの点について、AWS から公開されている 2 本の論文をベースにして解説を行いました。VPC Rechability / Network Access Analyzer は内部的には AWS Tiros と呼ばれるエンジンがクエリ処理を担っており、さらにそのバックエンドとして SMT ソルバの MonoSAT を使用しています。これに加え「不通の原因部分を含む完全な経路」をユーザに提示するため、与えられた制約をいくつかのクラスに分類し、段階的に Minimal Correction Subset (MCS) を計算する手法が用いられています。
補足
講演動画を見た方向けの補足です。スライド中に、MonoSAT のパフォーマンスについて「10 万(EC2)インスタンスで数 100 秒 〜 1,000 秒」と記載した部分があります。この情報について、講演では咄嗟に「単位の間違いでは」と言ってしまいましたが、グラフを見ればわかる通り間違いではありません。このデータは MonoSAT の規模的な限界性能、かつ Soufflé では解けないベンチマークの例として挙げられています。
Twitter の反応
現地登壇ということもあってか、今回はなんだか語り口が好評でした。この記事を読まれている方は、スライドだけでなく動画をご覧いただくと良いかもしれません。
VPC Reachability Analyzer と VPC Network Access Analyzer 知らなかった... 使いどころによってはこの二つもとても便利そう #CNDT2022 #CNDT2022_B
— Kei IWASAKI (@laugh_k) 2022年11月22日
実際に疎通しているわけではなく、ある変更を加えると通る。ある変更はユーザ変更可能箇所を MCS で特定する。から、traceroute のように断箇所でプツリと切れずにフィードバックされる…(最初の疑問)。後でもう一回見直そう。。。#CNDT2022 #CNDT2022_B
— Keisuke SAKASAI (@k6s4i53rx) 2022年11月22日
まさに「推理」という内容だった。スライドとチェシャ猫さんの話語りで楽しく聞けたしめっちゃおもしろかったです! #CNDT2022 #CNDT2022_B
— Kei IWASAKI (@laugh_k) 2022年11月22日
高度な内容を推理小説ばりに面白く解説頂きました!#CNDT2022 #CNDT2022_B
— yusuke nishikawa (@ukun2190_) 2022年11月22日
VPC Network Analyzerめっちゃ有能やん。その背後の学術的手法を丁寧に解説してくれてめちゃくちゃ面白かった。 🗣️(初歩的なことだよ、ワトソン君) #CNDT2022 #CNDT2022_B https://t.co/i5tojxqVCq
— なべ (@iho9z2qywfzt20w) 2022年11月22日
職人技ではなく数理による問題解決おもしろい👀#CNDT2022 #CNDT2022_B
— trunkatree (@trunkatree) 2022年11月22日
参考文献
- VPC Reachability Analyzer
- VPC Network Access Analyzer
- MonoSAT
- Backes, John, Sam Bayless, Byron Cook, Catherine Dodge, Andrew Gacek, Alan J. Hu, Temesghen Kahsai, et al. 2019. “Reachability Analysis for AWS-Based Networks.” In Computer Aided Verification, 231–41. Springer International Publishing. https://doi.org/10.1007/978-3-030-25543-5_14
- Bayless, S., J. Backes, D. DaCosta, B. F. Jones, N. Launchbury, P. Trentin, K. Jewell, S. Joshi, M. Q. Zeng, and N. Mathews. 2021. “Debugging Network Reachability with Blocked Paths.” In Computer Aided Verification, 851–62. Springer International Publishing. https://doi.org/10.1007/978-3-030-81688-9_39
おまけ:デモ環境の作成
以下の CloudFormation テンプレートを使用することで、VPC Reachability Analyzer と VPC Network Access Analyzer による分析を実際に試してみることができます。
このテンプレートの使用によって発生した問題には責任は持てません。特に、小さいとはいえ ECS インスタンスを実際に立てること、および両 Analyzer ともに有料(特に Reachability Analyzer は実行ごとに 0.1 USD と高価)である点にはご注意ください。
--- Description: 'Demo for CloudNative Days Tokyo 2022' AWSTemplateFormatVersion: 2010-09-09 Mappings: RegionMap: ap-northeast-1: execution: ami-02892a4ea9bfa2192 Resources: VPC: Type: AWS::EC2::VPC Properties: CidrBlock: 172.0.0.0/16 InternetGateway: Type: AWS::EC2::InternetGateway InternetGatewayAttachement: Type: AWS::EC2::VPCGatewayAttachment Properties: InternetGatewayId: !Ref InternetGateway VpcId: !Ref VPC SubnetX: Type: AWS::EC2::Subnet Properties: VpcId: !Ref VPC CidrBlock: 172.0.1.0/24 SubnetY: Type: AWS::EC2::Subnet DependsOn: InternetGateway Properties: VpcId: !Ref VPC CidrBlock: 172.0.2.0/24 MapPublicIpOnLaunch: true PublicRouteTable: Type: AWS::EC2::RouteTable Properties: VpcId: !Ref VPC PublicRouteTableAssociation: Type: AWS::EC2::SubnetRouteTableAssociation Properties: RouteTableId: !Ref PublicRouteTable SubnetId: !Ref SubnetY PublicRoute: Type: AWS::EC2::Route Properties: RouteTableId: !Ref PublicRouteTable GatewayId: !Ref InternetGateway DestinationCidrBlock: 0.0.0.0/0 SecurityGroup1: Type: AWS::EC2::SecurityGroup Properties: GroupDescription: 'Sample SG 1' VpcId: !Ref VPC SecurityGroupIngress: - CidrIp: !GetAtt VPC.CidrBlock IpProtocol: 'tcp' FromPort: 22 ToPort: 22 SecurityGroupEgress: - CidrIp: 0.0.0.0/0 IpProtocol: '-1' SecurityGroup2: Type: AWS::EC2::SecurityGroup Properties: GroupDescription: 'Sample SG 2' VpcId: !Ref VPC SecurityGroupIngress: - CidrIp: !GetAtt VPC.CidrBlock IpProtocol: 'tcp' FromPort: 22 ToPort: 22 SecurityGroupEgress: - CidrIp: 127.0.0.1/32 IpProtocol: '-1' InstanceA: Type: AWS::EC2::Instance Properties: ImageId: Fn::FindInMap: - RegionMap - !Ref AWS::Region - execution InstanceType: 't3.nano' SubnetId: !Ref SubnetX SecurityGroupIds: - !Ref SecurityGroup1 Tags: - Key: Name Value: InstanceA InstanceB: Type: AWS::EC2::Instance Properties: ImageId: Fn::FindInMap: - RegionMap - !Ref AWS::Region - execution InstanceType: 't3.nano' SubnetId: !Ref SubnetX SecurityGroupIds: - !Ref SecurityGroup2 Tags: - Key: Name Value: InstanceB InstanceC: Type: AWS::EC2::Instance Properties: ImageId: Fn::FindInMap: - RegionMap - !Ref AWS::Region - execution InstanceType: 't3.nano' SubnetId: !Ref SubnetY SecurityGroupIds: - !Ref SecurityGroup1 Tags: - Key: Name Value: InstanceC ReachablePath: Type: AWS::EC2::NetworkInsightsPath Properties: Source: !Ref InstanceA Destination: !Ref InstanceC DestinationPort: 22 Protocol: tcp Tags: - Key: Name Value: 'Reachable Path' BlockedPath: Type: AWS::EC2::NetworkInsightsPath Properties: Source: !Ref InstanceB Destination: !Ref InstanceC DestinationPort: 22 Protocol: tcp Tags: - Key: Name Value: 'Blocked Path' AccessToInternet: Type: AWS::EC2::NetworkInsightsAccessScope Properties: MatchPaths: - Destination: ResourceStatement: ResourceTypes: - AWS::EC2::InternetGateway Tags: - Key: Name Value: 'All Access To Internet'
AWS Dev Day 2022 Japan に「サーバーレスは操作的意味論の夢を見るか?」というタイトルで登壇してきました
こんにちは、チェシャ猫です。
先日開催された AWS Dev Day 2022 Japan で、サーバーレスコンピューティングの形式化について発表してきました。公募 CFP 枠です。
ちなみに会場は観葉植物が生い茂る Amazon 品川オフィスで、講演者向けには個室の楽屋が用意されており(滞在時間は講演直前の 15 分程度ですが)、全体的にとてもゴージャスな感じでした。配信設備も本格的でしたが、話す側としては照明が眩しくてやりづらかったです。
講演概要
AWS Lambda を初めとするサーバーレスコンピューティング基盤には、
- 複数の関数が同時に実行され共有リソースにアクセスしうる、本質的に並行システムである
- Warm Start により関数インスタンスが内部状態を残したまま再利用されうる
- 一つのリクエストに対して複数回の実行が行われうる、いわゆる At-Least-Once 特性
といった特性があり、通常のプログラムと比較して実行モデルが複雑かつアンコントローラブルな要素を多く含みます。関数を実装する側はこのような「プラットフォームの都合」を考慮して冪等性など細かい挙動に気を配りつつプログラムを書くことになり、これは一般にかなりの実装コストになります。また、アンコントローラブルな要素は、関数の実装から実際の挙動を静的に検査することを難しくしています。
このような問題に対して、Jangda らは 2019 年、サーバーレスコンピューティング自体に形式的な基礎付けを与えた論文 "Formal Foundations of Serverless Computing" を発表しました。今回の講演はこの論文、特に前半部分に焦点を当てたものです。上記の「プラットフォームの都合」を織り込んだサーバーレスの意味論、およびより直感的な挙動を表現した単純化された意味論の 2 種類を定義し、両者が弱双模倣の関係となる条件を記述するところまでを解説しました。
今回の講演の主眼は論文紹介ではありますが、あくまでも計算機科学に馴染みがない参加者に向けたものであり、「操作的意味論とは」といった入門者向けの内容も含め解説しています。参加者の次のステップにつなげてもらおうという意図から、最後には「次に読む本」としてプログラム意味論関係の参考書をいくつか挙げました。
スライド冒頭でも述べていますが、普段この分野に縁遠い方が、講演をきっかけに「ちょっと本でも読んでみるか」となればチェシャ猫の勝利です。以上、よろしく。
次に読むおすすめ書籍
Twitter の反応
「サーバーレスは操作的意味論の夢を見るか?」めちゃくちゃすげえこと言ってる。面白すぎる。アーカイブって出るのかな?#AWSDevDay
— なべ (@iho9z2qywfzt20w) 2022年11月10日
11月中読破目指す pic.twitter.com/sIqnh4iYxO
— なべ (@iho9z2qywfzt20w) 2022年11月15日
#AWSDevDay Eトラックやべー。
— mashiike (@mashiike) 2022年11月10日
この論文の解説が偉大すぎる
#AWSDevDay 意味論ほぼ初見だから頭爆発するかと思ったけどメチャクチャ面白いなコレ……。
— 吉村美代 (@myonyomu) 2022年11月10日
【E-2】サーバーレスは操作的意味論の夢を⾒るか。内容がほぼ理解出来ない俺は悪夢を見た気がする。とりあえず、おすすめ書籍をポチるか・・。記憶しているセッションで一番の衝撃だった #AWSDevDay
— Makoto Tezuka (@tezu33) 2022年11月10日
参考文献
- Abhinav Jangda, Donald Pinckney, Yuriy Brun, and Arjun Guha. 2019. "Formal foundations of serverless computing." Proc. ACM Program. Lang. 3, OOPSLA, Article 149 (October 2019), 26 pages.
- Maurizio Gabbrielli, Saverio Giallorenzo, Ivan Lanese, Fabrizio Montesi, Marco Peressotti and Stefano Pio Zingaro. 2019. "No more, no less - A formal model for serverless computing." COORDINATION.
- Matthew Obetz, Anirban Das, Timothy Castiglia, Stacy Patterson, and Ana Milanova. 2020. “Formalizing Event-Driven Behavior of Serverless Applications.” In Service-Oriented and Cloud Computing, 19–29. Springer International Publishing.
- 五十嵐淳 (2011). プログラミング言語の基礎概念. サイエンス社.
- 小林直樹, 住井英二郎 (2020). プログラム意味論の基礎. サイエンス社.
- Tom Stuart (2013). Understanding Computation. O'Reilly Media, Inc. 邦訳あり
2021 年のアウトプットを全部一気に思い出す
こんにちは、チェシャ猫です。2021 年中は大変お世話になりました。
今年もいくつか外部で発表を行いましたが、その中には登壇報告の形でこのブログに載せていなかったり、スライドとして公開していないものがあります。自分自身の記録も兼ねて、本記事では 2021 年のアウトプットを一覧としてアーカイブしておきたいと思います。

2021 年の活動実績
2021 年の登壇は 9 件でした。うち(先着や抽選ではなく)CFP に応募して採択されたものは 5 件 です。傾向として以前よりも LT の割合が少なくなり、比較的長尺の登壇がメインになりました。
- CockroachDB から覗く型式手法の世界【CFP 採択】
- ポリシエンジン Kyverno 入門
- containerd をソースコードレベルで理解する
- containerd をソースコードレベルで理解する(再演)
- Infrastructure as Code の静的テスト戦略【CFP 採択】
- Kubewarden を使って任意の言語でポリシを書こう
- AWS セキュリティは「論理」に訊け! Automated Reasoning の理論と実践【CFP 採択】
- 君のセキュリティはデプロイするまでもなく間違っている【CFP 採択】
- ネットワークはなぜつながらないのか 〜インフラの意味論的検査を目指して〜【CFP 採択】
また、登壇報告以外に単独の記事を 1 件 書きました。Zenn デビュー作です。今後はこちらも拡充していければと思います。
以下、個々の内容について簡単な解説コメントを交えて振り返ります。
CockroachDB から覗く型式手法の世界
July Tech Festa 2021 winter での発表です。録画はこちら。
CockroachDB の Parallel Commit の設計に TLA+ が使用された事例について、形式手法が必要とされる理由、Parallel Commit のプロトコル、および実際に使用されている TLA+ の言語機能について解説しています。
内容は CloudNative Days Tokyo 2020 で話した同タイトルのスライドをほぼ踏襲していますが、時間が 10 分伸びたため、CockroachDB 以外の TLA+ 採用事例や分散システムにおける Chaos Engineering の位置付けについて解説を追加しました。
本当は TiDB や Azure Cosmos DB、elasticsearch などの話を盛り込んで「データベースと形式手法」的なコンテンツにする予定だったのですが、時間との兼ね合いで最終的には CockroachDB に絞ることになりました。
ポリシエンジン Kyverno 入門

Kubernetes Meetup Tokyo #40 での発表です。録画はこちら。
Kubernetes 向けに Policy as Code を実装する場合、現状では Open Policy Agent (OPA) とその関連ツールがデファクトスタンダートになっています。しかし OPA はポリシの記述に Prolog ベースの Rego 言語の知識を要求するため、組織内で横展開しようとすると学習コストの高さが問題になります。
この学習コスト問題をどうにかしようとして登場したツールの一つが Kyverno です。Kyverno ではポリシを YAML で記述します。YAML なのでロジックの表現力には劣りますが、Rego よりも手軽に記述することができます。さらに、Rego の記述を文字列として Manifest に埋め込む OPA と異なり、YAML であれば Kubernetes のリソースとして自然な統合が可能です。
という話をしようと思ったのですが、なんとちょうど前日に 別の方が他のイベントで Kyverno に関する LT をされていた ため、自分からは特に説明する内容がなくなりました。まあ人生、そんな日もあります。
containerd をソースコードレベルで理解する

CloudNative Days Spring 2021 ONLINE での発表です。録画はこちら。
Pod を起動させる際、Kubernetes は Container Runtime Interface (CRI) というインターフェスに従い、gRPC 経由で外部ランタイムに処理を移譲します。containerd や CRI-O は CRI ランタイムの例です。
この発表では、containerd の CRI 関連部分に絞って、Pod 起動の際に辿る処理の流れをソースコードベースで解説しています。
ソースコードの構造を理解する上で鍵になるのは、containerd の Modular Monolith 的なアーキテクチャです。バイナリとしては一つにまとめてビルドされていますが、各モジュールが処理を他のモジュールに移譲する際、直接相手のメソッドを呼ぶのではなく、クライアントを経由してあたかも外部サーバへのアクセスであるかのように呼び出します。
containerd をソースコードレベルで理解する(再演)

Kubernetes Internal #7 での発表です。録画はこちら。
解説の流れは上記の CloudNative Days Spring 2021 ONLINE とほぼ同じです。
スライドの表紙が「ちょっと詳しい版」となっていますが、実際にはスライド自体にはほとんど差はありません。Kubernetes Internal は Discord を使用し双方向で進めることができるので、聴衆の反応を反応を見つつ、アドリブで追加説明を入れたり GitHub 上の関連プロジェクトなどを紹介したりしています。
Infrastructure as Code の静的テスト戦略
DevOpsDays Tokyo 2021 での発表です。
内容・スライドは CloudOperatorDays Tokyo 2020 でお話しした内容をおおむね踏襲し、細かい部分に時間経過に伴う更新を入れました。
「Infrastructure as Code を実践しようとしたが、なかなかスムーズにいかなくて辛い」というのは大なり小なり覚えがあるところだと思います。
発表の前半ではこの問題を言語化するために「予測可能性」という考え方を導入しました。さらに後半では AWS を取り上げ、予測可能性を担保するための方法論や具体的なツールの適用について解説しています。
この発表は、ものすごく久しぶりのオンサイト登壇になったという意味で、個人的には思い出深いものです。マイクを持って物理的に対面して話すのことの効果は大きく、久々に自分の本来のペースが出せたので非常に良かったです。
なお、この発表はログミー Tech にて全 3 回に分けて書き起こしが掲載されています。
Kubewarden を使って任意の言語でポリシを書こう
Kubernetes Meetup Tokyo #42 での発表です。録画はこちら。
Kyverno に引き続き、Kubernetes 向け Policy as Code に関する発表の第二弾です。
ポリシを YAML で記述する Kyverno と異なり、Kubewarden は WebAssembly で記述します。そのため、WebAssembly が生成できる言語なら何でも(理屈の上では)利用可能で、タイトルに「任意の言語で」と入れたのはこれを意図しています。スライド中では Go (TinyGo) で書く場合を例として取り上げました。
AWS セキュリティは「論理」に訊け! Automated Reasoning の理論と実践
July Tech Festa 2021 での発表です。録画はこちら。
SMT ソルバ Z3 を利用して AWS の権限周りを検査する推論エンジン、Zelkova について解説しました。
Zelkova は AWS IAM Access Analyzer や AWS Config に統合されており、危険なアクセスを許可していないかを自動で保証することができます。
元になっている論文は以下です。
July Tech Festa は 20 分しか枠がないこともあり、スライドの最後のほう、論文に述べられた SMT エンコーディングを解説する部分がちょっと消化不良になってしまいました。この反省点は、次に挙げる CI/CD Conference 2021 で活かされています。
なお、この発表はログミー Tech にて書き起こしが掲載されています。
君のセキュリティはデプロイするまでもなく間違っている
CI/CD Conference 2021 での発表です。録画はこちら。
July Tech Festa 2021 と同じく、Zelkova による AWS 上のセキュリティ検証の仕組みを解説しています。
前回が 20 分枠だったのに比較してこちらは 40 分枠なので、同じ題材でもより分かりやすく解説することができたと自負しています。特に後半、IAM Policy の意味論を SMT ソルバ用にエンコードする部分について、順を追って必要な仕組みを整理してあります。
ネットワークはなぜつながらないのか 〜インフラの意味論的検査を目指して〜
AWS Dev Day Online Japan 2021 での発表です。録画はこちら。
SMT ソルバを利用して AWS のネットワーク周りを検査する推論エンジン、Tiros について解説しました。
Tiros はこの登壇時点で VPC Reachability Analyzer や Amazon Inspector に統合済みでした。2021 年 12 月には VPC Network Access Analyzer も提供されており、単なる到達性だけでなく、ネットワークが無闇に解放されていないかどうかをセキュリティの観点から確認することもできるようになっています。
元になっている論文は以下です。
この論文では、AWS のネットワークを検査する上で採用するエンジンとして、Datalog の処理系 Soufflé、SMT ソルバ MonoSAT および一階述語論理の自動定理証明器 Vampire の三種類を比較をしています。実際に採用されたのは MonoSAT で、MonoSAT はグラフについての理論が実装されている点が特徴です。
Alloy 6 の新機能 Mutable Field と線形時相論理
仕様記述言語 Alloy に関する新機能の紹介記事です。
v6 より前の Alloy には時間発展を記述する機能がありません。そのためユーザが「時間に従って変化する仕様」を記述する際には、明示的に時間をシグネチャとして導入する必要がありました。実際のシステムの仕様を記述する上で時間発展は頻出であり、慣れれば難しくはないのですが、細かいはまりどころがあったりして不便です。またビジュアライザがそれ用に作られているわけではないので、結果が見づらいという問題もあります。
2021 年 11 月にリリースされた Alloy 6 は、Mutable Field と呼ばれる記法を導入することでこの問題を解決しました。また、ビジュアライザにも状態遷移の前後が並べて表示できるなどの改善が加えられました。さらに、検査したい述語として線形時相論理式が使用できるようになっています。
まとめ
以上、本記事では 2021 年の登壇 9 件と記事 1 件について、簡単なコメントと共に振り返りました。
記事 1 件はやや寂しいですね。実は Alloy 以外にも Zenn に載せる用に検証を進めていた題材がいくつかあったのですが、結局どれも問題があって記事化には至りませんでした。
- 文章を書くタイプのアウトプットにもう少しウェイトを振る
- どこかのイベントで発表するだけでなく、自分自身が保有する情報発信チャンネルを確立する
あたりが来年の活動方針かなと考えています。
それでは、2022 年も張り切っていきましょう。よろしくお願いいたします。
VPC Reachability Analyzer と形式手法
こんにちは、チェシャ猫です。
先日開催された AWS Dev Day Online Japan 2021 で、AWS の VPC Reachability Analyzer とそのバックエンドである Tiros について発表してきました。公募 CFP 枠です。
講演概要
このプレゼンの大きな目標は、VPC Reachability Analyzer のバックエンドである検査エンジン Tiros の論文 [Bac19] を解説することです。そのための道筋として、Section 1 で VPC Reachability Analyzer の機能を簡単に紹介した後、Section 2 でその要素技術である SMT ソルバの仕組みを解説し、最後に Section 3 として VPC ネットワークの意味論を SMT ソルバ用にエンコーディングする方針について解説します。
VPC Reachability Analyzer
AWS 上でネットワークが意図通りの挙動を示さない時、トラブルシュートには二つの方針があります。一つは nc をはじめとするネットワーク形のコマンドを用いて実際にパケットを送信してみることであり、もう一つは AWS マネジメントコンソールから設定ミスを見つけることです。しかし、実際にこの辺りのトラブルシュートを経験したことがある方はご存知の通り、いずれもそれなりの前提知識が必要で、いわゆる「職人芸」になりがちな部分でもあります。
2020 年 12 月、そんなトラブルシューティングに便利な機能が AWS から発表されました。VPC Reachability Analyzer です。この機能では、通信の送信元と送信先を指定することで、その間の通信が到達可能になるかどうかを自動的に判定することができます。また、到達可能でない場合には原因となっているコンポーネントの特定も可能です。

VPC Reachability Analyzer が面白いのは、Packet Probing と呼ばれる実際にパケットの送信を行うタイプの古典的な検査とは異なり、設定項目のみからを読み取って推論を行うところです。いわば AWS のネットワーク設定が持つ「意味」を理解して結論を出しているとも言えます。この特徴があるため、実際のプロダクション環境で検査を行っても帯域に悪影響を与えることがなく、また到達不可能な場合に「どこを修正すれば到達できるか」まで含めた情報を得ることができます。
VPC Reachability Analyzer については、今回解説する論文の他にも AWS からいくつか資料が出てきます。
- 新機能 – VPC Reachability Analyzer | Amazon Web Services ブログ
- AWS re:Invent 2019: Provable access control: Know who can access your AWS resources (SEC343-R) - YouTube
SAT ソルバと SMT ソルバ
それでは、VPC Reachability Analyzer が実際の通信を行うことなく到達性を「推論」できるのはなぜでしょうか? この秘密は内部で SMT ソルバを呼び出していることにあります。
SMT ソルバの前提として、まず SAT ソルバについて押さえておきましょう。SAT ソルバは命題論理式の充足可能性(SATisfiability)、すなわち各変数にうまい真偽値を割り当てることで与えられた式の全体が真にできるかどうかを判定するソルバです。SAT 問題とそのソルバのアルゴリズムは古くから研究される対象であり、さまざまな高速化が知られています。反面、命題論理式しか扱うことができないため、現実の問題をエンコードすると問題のサイズが大きくなりすぎたり、元の問題の構造を失ってしまうために非効率になることも少なくありません。
このような SAT ソルバの欠点を補完して実用を意図したパフォーマンスを出すツールとして、SMT ソルバがあります。SMT ソルバでは特定の理論のソルバを別途用意します。理論に関連した部分式を命題変数に抽象化した上で、論理演算の部分のみ SAT ソルバが解き、結果を理論ソルバに渡すことで残りの部分式を解かせるという連携を行います。
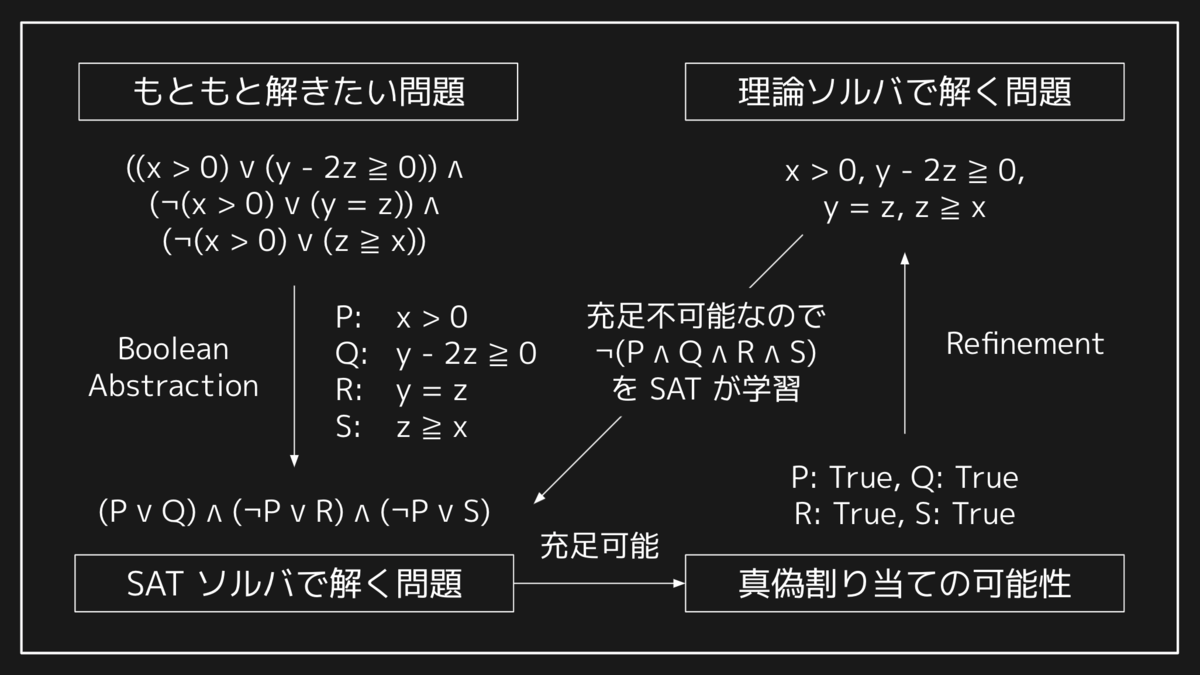
実際には、現代の実用的な SMT ソルバでは SAT 部分と理論部分は完全に独立して動作するわけではなく、SAT ソルバが命題変数への真偽割り当てを探索する過程で理論ソルバのアルゴリズムが介入することで探索空間を減らし、パフォーマンスを上げる工夫が入っています。このようなタイプの SMT ソルバは Lazy SMT と呼ばれたりします。
このあたりの詳細に興味がある人は、参考文献 [Seb07] を参照してください。Lazy SMT に関する包括的なサーベイ論文です。
MonoSAT によるエンコーディング
AWS の内部でも SMT ソルバが使用されています。冒頭に挙げた VPC Reachability Analyzer もその一つで、Tiros と呼ばれる内部のエンジンが SMT ソルバの一種である MonoSAT をバックエンドとして使用しています。
論文中には、Tiros は MonoSAT 以外の実装の候補として、Datalog 処理系 Soufflé [Sub19] と一階述語論理の自動定理証明器 Vampire [Kot18] が提案されており、それぞれが VPC をどのようにモデル化したのかについて述べられています。大規模ベンチマークの結果としては MonoSAT が多くの場合に最速ですが、Soufflé では MonoSAT では実装できないタイプのクエリが存在する点に言及されています。具体的には純粋なネットワークの接続以外の、例えば EC2 インスタンスのタグに言及するようなクエリがその例です。
Tiros が MonoSAT を用いて VPC ネットワークの意味論を検査するさいには、MonoSAT が持っているグラフ理論用の理論ソルバを使用します。具体的には EC2 インスタンスや ENI、セキュリティグループなどのコンポーネントをノードとし、ENI とセキュリティブループ間のようなアタッチ関係をエッジとします。このとき、やはり MonoSAT が持つビットベクトルの理論ソルバを使ってコンポーネントを通過できるパケット条件を記述することで、パケットの到達可能性はグラフの到達可能性として検査することが可能になります。
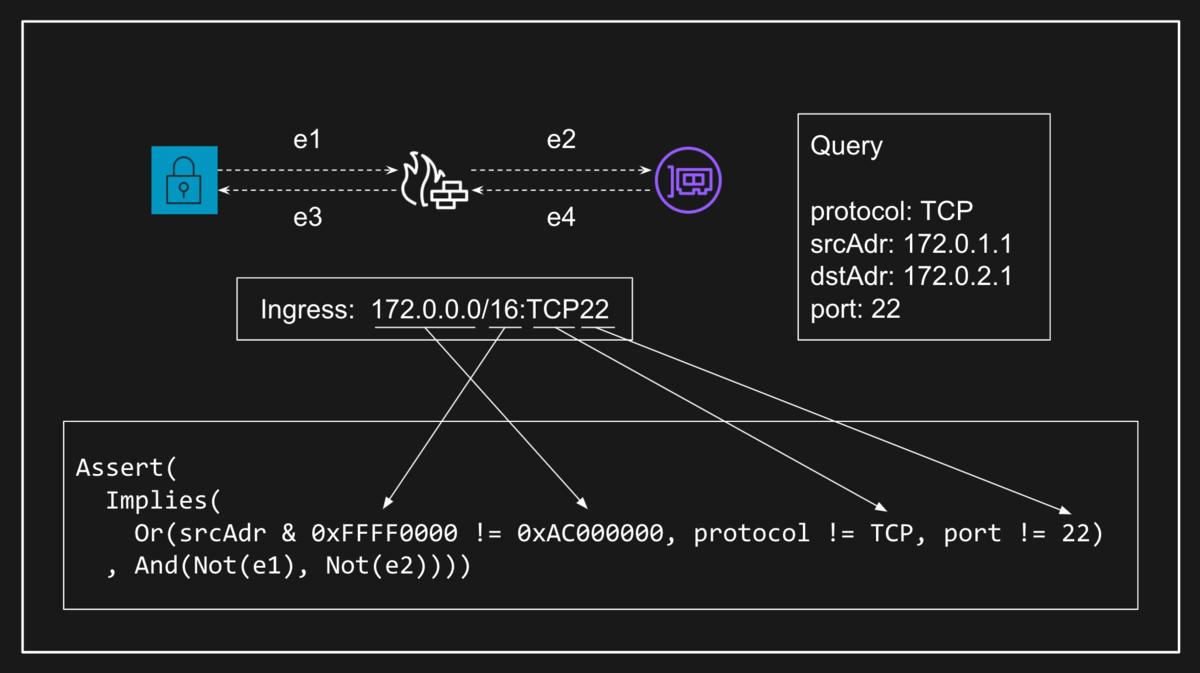
ところで、MonoSAT が持つグラフ理論の理論ソルバは、汎用の SMT ソルバとしては特殊なものです。逆に言えばなぜ MonoSAT はグラフの理論ソルバを実装しているのでしょうか?
この答えは MonoSAT の提案論文である参考文献 [Bay15] に述べられています。ここで鍵になるのはと Boolean Monotonic Theories と呼ばれる理論のクラスです。Boolean Monotonic な理論では述語や関数の引数が真偽値に限定されており、かつ述語 に対して以下の性質が成り立ちます。
つまり、その述語がある変数を偽としたときに成立するのであれば、その変数を真に変えたときでもやはり成立する、という性質です。
今回考えているグラフの到達可能性は、この Monotonic の性質を満たす述語です。実際、あるエッジが偽(接続しない)の状態で到達可能なノード同士は、そのエッジを真(接続する)に変更したとしてもやはり到達可能です。また、MonoSAT が実装している到達性以外の述語、例えば最小スパニング木の生成などについてもこの性質が成り立ちます。
理論が Monotonic である場合、理論ソルバ側の原子命題への部分的な真偽割り当てが与えられた段階で、残りをすべて真で埋めてしまって理論ソルバで検証することが可能になります。なぜなら、そうして得られた結果が充足不可能であれば、部分的な割り当ての時点で既に充足不可能であることがわかるからです。逆に、すべて偽で埋めた状況で充足可能が確定すれば、残りの変数の真偽はどちらでも問題ないことがわかります。いわば、上下からおおざっぱな評価をしてみて情報を引き出していると言えるでしょう。これを利用して探索空間を絞るのが MonoSAT の、ひいては Tiros の戦略です。
Blocked Path の検出
これは当日のプレゼンに入れられなかった補足なのですが、今年に入ってから Tiros の機能を拡張する論文 [Bay21] が出ており、しかもこの論文は VPC Reachability Analyzer に直接関係しています。具体的には、接続できない場合に原因となっているコンポーネントを検出する方法について示した論文です。
一般には、MonoSAT で到達不可能であることが示された場合、何が原因であるかは明らかではありません。理論ソルバ側が充足不可能だった場合には矛盾が生じた式の集合を返してくるため、そこから修正すべき原因を引き出してユーザに情報を提示することになります。
ここで一筋縄でいかないのは、最終的な出力として何を残す必要があるかによってアルゴリズムが変わることです。前述の論文ではこの「到達不可能な原因」を以下の 3 種類に分類しています。
そして、それぞれに対して「最小の矛盾集合」を段階的に得るアルゴリズムとその正当性を示す流れが論文の骨子です。
サンプル構成
今回サンプルとして使用した EC2 インスタンス 3 個からなる構成は、以下の CloudFormation テンプレートから作成することができます。なお、このテンプレートを使用することで生じた問題には一切責任は持てません。特に、小さいとはいえ実際のインスタンスを立てること、また VPC Reachability Analyzer の実行には安くない料金(0.1 USD / 検査)がかかることに注意してください。
--- Description: 'Demo for AWS Dev Day 2021: Breakout Session G-4' AWSTemplateFormatVersion: 2010-09-09 Mappings: RegionMap: ap-northeast-1: execution: ami-02892a4ea9bfa2192 Resources: VPC: Type: AWS::EC2::VPC Properties: CidrBlock: 172.0.0.0/16 SubnetX: Type: AWS::EC2::Subnet Properties: VpcId: !Ref VPC CidrBlock: 172.0.1.0/24 SubnetY: Type: AWS::EC2::Subnet Properties: VpcId: !Ref VPC CidrBlock: 172.0.2.0/24 SecurityGroup1: Type: AWS::EC2::SecurityGroup Properties: GroupDescription: 'Allow SSH from inside of the VPC' VpcId: !Ref VPC SecurityGroupIngress: - CidrIp: !GetAtt VPC.CidrBlock IpProtocol: "tcp" FromPort: 22 ToPort: 22 SecurityGroupEgress: - CidrIp: 0.0.0.0/0 IpProtocol: "-1" SecurityGroup2: Type: AWS::EC2::SecurityGroup Properties: GroupDescription: 'Deny all incomming accesses' VpcId: !Ref VPC SecurityGroupEgress: - CidrIp: 0.0.0.0/0 IpProtocol: "-1" InstanceA: Type: AWS::EC2::Instance Properties: ImageId: Fn::FindInMap: - RegionMap - !Ref AWS::Region - execution InstanceType: 't3.nano' SubnetId: !Ref SubnetX SecurityGroupIds: - !Ref SecurityGroup1 Tags: - Key: Name Value: InstanceA InstanceB: Type: AWS::EC2::Instance Properties: ImageId: Fn::FindInMap: - RegionMap - !Ref AWS::Region - execution InstanceType: 't3.nano' SubnetId: !Ref SubnetY SecurityGroupIds: - !Ref SecurityGroup1 Tags: - Key: Name Value: InstanceB InstanceC: Type: AWS::EC2::Instance Properties: ImageId: Fn::FindInMap: - RegionMap - !Ref AWS::Region - execution InstanceType: 't3.nano' SubnetId: !Ref SubnetY SecurityGroupIds: - !Ref SecurityGroup2 Tags: - Key: Name Value: InstanceC ReachablePath: Type: AWS::EC2::NetworkInsightsPath Properties: Source: !Ref InstanceA Destination: !Ref InstanceB DestinationPort: 22 Protocol: tcp UnreachablePath: Type: AWS::EC2::NetworkInsightsPath Properties: Source: !Ref InstanceA Destination: !Ref InstanceC DestinationPort: 22 Protocol: tcp
まとめ
以上、AWS の VPC ネットワークにおいて、トラブルシューティングを自動化するのに便利な機能 VPC Reachability Analyzer と、そのバックエンドである Tiros、さらにその背後にある SMT ソルバ MonoSAT の特性について解説しました。
ところで、ベンチマークのスライドで述べている通り、MonoSAT は複数の経路が存在するようなケースで性能が悪化することが知られています。これは MonoSAT に限らず、一般に SMT ソルバベースのソリューションで見られる傾向です。このような場合に極力パフォーマンスを悪化させないために、Header Space Analysis と呼ばれる手法も知られているのですが、それはまた別の話。
参考文献
- [Bac19] Backes, John, Sam Bayless, Byron Cook, Catherine Dodge, Andrew Gacek, Alan J. Hu, Temesghen Kahsai, et al. 2019. “Reachability Analysis for AWS-Based Networks.” In Computer Aided Verification, 231–41. Springer International Publishing.
- [Bay15] Bayless, Sam, Noah Bayless, Holger Hoos, and Alan Hu. 2015. “SAT Modulo Monotonic Theories.” Proceedings of the AAAI Conference on Artificial Intelligence 29 (1). https://ojs.aaai.org/index.php/AAAI/article/view/9755.
- [Bay21] Bayless, S., J. Backes, D. DaCosta, B. F. Jones, N. Launchbury, P. Trentin, K. Jewell, S. Joshi, M. Q. Zeng, and N. Mathews. 2021. “Debugging Network Reachability with Blocked Paths.” In Computer Aided Verification, 851–62. Springer International Publishing.
- [Kot18] Kotelnikov, Evgenii. 2018. “Automated Theorem Proving with Extensions of First-Order Logic.” search.proquest.com. https://search.proquest.com/openview/2407fa8ebeb24157d4348884a5d03dd5/1?pq-origsite=gscholar&cbl=18750&diss=y.
- [Seb07] Sebastiani, Roberto. 2007. “Lazy Satisfiability Modulo Theories.” Journal on Satisfiability, Boolean Modeling and Computation 3 (3-4): 141–224.
- [Sub19] Subotic, Pavle. 2019. “Scalable Logic Defined Static Analysis.” Doctoral, UCL (University College London). https://discovery.ucl.ac.uk/id/eprint/10067190/.
CI/CD Conference 2021 で Zelkova の論文について話してきました
こんにちは、チェシャ猫です。
先日開催された CI/CD Conference 2021 で、AWS の IAM Access Anazlyer のバックエンドとして使用されている検査エンジン Zelkova、およびその元となった論文について発表してきました。公募 CFP 枠です。
発表の大筋は、少し前に July Tech Festa 2021 で登壇した際のものと共通です。関連リンク集などは以下の記事にまとめてあるので、よかったらこちらも合わせてお読みください。
内容面では、前回の発表時間 20 分に対して今回は 40 分の枠をもらっていたので、
- Level 1-3 として定式化した「検査水準」とツールの対応を明確にすること
- Zelkova による IAM Policy の SMT エンコードについてより具体的に述べること
の 2 点を中心に内容の整理・再構成を行いました。特に後者についてはスライドの構成に大幅に手を入れたので、前回よりかなり分かりやすいプレゼンになったのではないかと自負しています。
なお、スライド中にも宣伝を入れた通り、AWS の「もう一つの推論エンジン」であるネットワーク検査エンジン Tiros については、AWS Dev Day Online 2021 で詳しくお話しする予定です。Z3 のみをバックエンドとする Zelkova と異なり、Tiros では MonoSAT、Soufflé、そして Vampire という複数のソルバを組み合わせて推論を行うのですが、それはまた別の話。