VPC Reachability Analyzer と形式手法 - チェシャ猫の消滅定理

こんにちは、チェシャ猫です。

先日開催された AWS Dev Day Online Japan 2021 で、AWS の VPC Reachability Analyzer とそのバックエンドである Tiros について発表してきました。公募 CFP 枠です。

www.youtube.com

講演概要

このプレゼンの大きな目標は、VPC Reachability Analyzer のバックエンドである検査エンジン Tiros の論文 [Bac19] を解説することです。そのための道筋として、Section 1 で VPC Reachability Analyzer の機能を簡単に紹介した後、Section 2 でその要素技術である SMT ソルバの仕組みを解説し、最後に Section 3 として VPC ネットワークの意味論を SMT ソルバ用にエンコーディングする方針について解説します。

VPC Reachability Analyzer

AWS 上でネットワークが意図通りの挙動を示さない時、トラブルシュートには二つの方針があります。一つは nc をはじめとするネットワーク形のコマンドを用いて実際にパケットを送信してみることであり、もう一つは AWS マネジメントコンソールから設定ミスを見つけることです。しかし、実際にこの辺りのトラブルシュートを経験したことがある方はご存知の通り、いずれもそれなりの前提知識が必要で、いわゆる「職人芸」になりがちな部分でもあります。

2020 年 12 月、そんなトラブルシューティングに便利な機能が AWS から発表されました。VPC Reachability Analyzer です。この機能では、通信の送信元と送信先を指定することで、その間の通信が到達可能になるかどうかを自動的に判定することができます。また、到達可能でない場合には原因となっているコンポーネントの特定も可能です。

VPC Reachability Analyzer が面白いのは、Packet Probing と呼ばれる実際にパケットの送信を行うタイプの古典的な検査とは異なり、設定項目のみからを読み取って推論を行うところです。いわば AWS のネットワーク設定が持つ「意味」を理解して結論を出しているとも言えます。この特徴があるため、実際のプロダクション環境で検査を行っても帯域に悪影響を与えることがなく、また到達不可能な場合に「どこを修正すれば到達できるか」まで含めた情報を得ることができます。

VPC Reachability Analyzer については、今回解説する論文の他にも AWS からいくつか資料が出てきます。

SAT ソルバと SMT ソルバ

それでは、VPC Reachability Analyzer が実際の通信を行うことなく到達性を「推論」できるのはなぜでしょうか？この秘密は内部で SMT ソルバを呼び出していることにあります。

SMT ソルバの前提として、まず SAT ソルバについて押さえておきましょう。SAT ソルバは命題論理式の充足可能性（SATisfiability）、すなわち各変数にうまい真偽値を割り当てることで与えられた式の全体が真にできるかどうかを判定するソルバです。SAT 問題とそのソルバのアルゴリズムは古くから研究される対象であり、さまざまな高速化が知られています。反面、命題論理式しか扱うことができないため、現実の問題をエンコードすると問題のサイズが大きくなりすぎたり、元の問題の構造を失ってしまうために非効率になることも少なくありません。

このような SAT ソルバの欠点を補完して実用を意図したパフォーマンスを出すツールとして、SMT ソルバがあります。SMT ソルバでは特定の理論のソルバを別途用意します。理論に関連した部分式を命題変数に抽象化した上で、論理演算の部分のみ SAT ソルバが解き、結果を理論ソルバに渡すことで残りの部分式を解かせるという連携を行います。

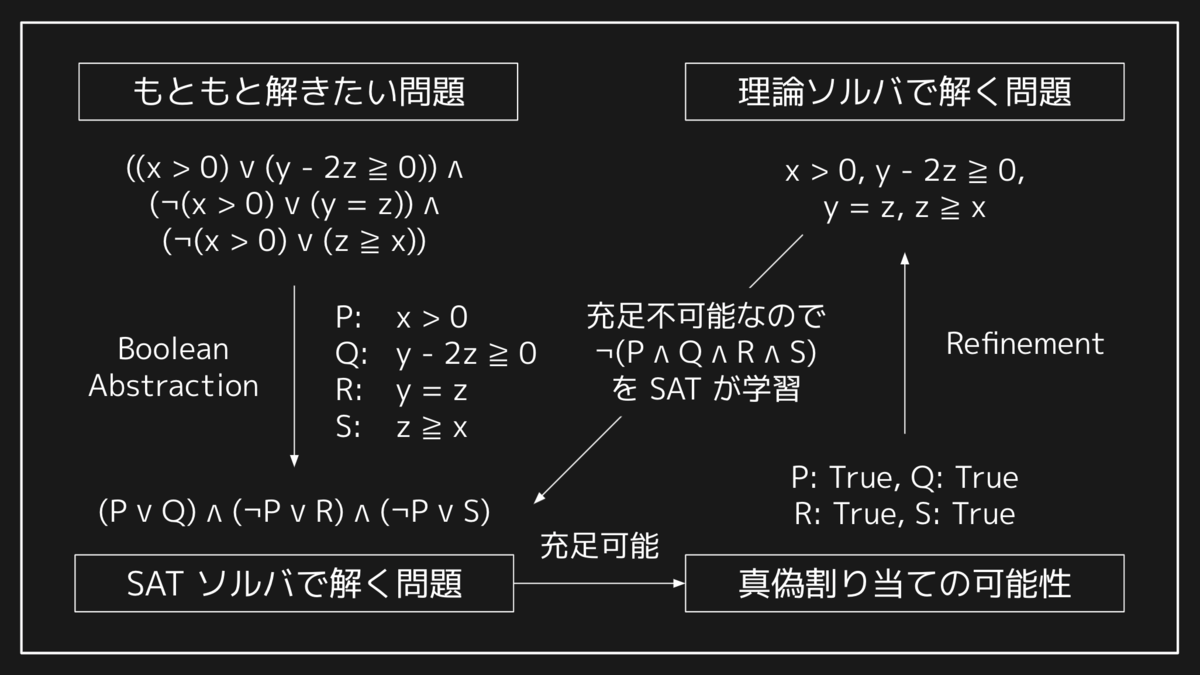
実際には、現代の実用的な SMT ソルバでは SAT 部分と理論部分は完全に独立して動作するわけではなく、SAT ソルバが命題変数への真偽割り当てを探索する過程で理論ソルバのアルゴリズムが介入することで探索空間を減らし、パフォーマンスを上げる工夫が入っています。このようなタイプの SMT ソルバは Lazy SMT と呼ばれたりします。

このあたりの詳細に興味がある人は、参考文献 [Seb07] を参照してください。Lazy SMT に関する包括的なサーベイ論文です。

MonoSAT によるエンコーディング

AWS の内部でも SMT ソルバが使用されています。冒頭に挙げた VPC Reachability Analyzer もその一つで、Tiros と呼ばれる内部のエンジンが SMT ソルバの一種である MonoSAT をバックエンドとして使用しています。

論文中には、Tiros は MonoSAT 以外の実装の候補として、Datalog 処理系 Soufflé [Sub19] と一階述語論理の自動定理証明器 Vampire [Kot18] が提案されており、それぞれが VPC をどのようにモデル化したのかについて述べられています。大規模ベンチマークの結果としては MonoSAT が多くの場合に最速ですが、Soufflé では MonoSAT では実装できないタイプのクエリが存在する点に言及されています。具体的には純粋なネットワークの接続以外の、例えば EC2 インスタンスのタグに言及するようなクエリがその例です。

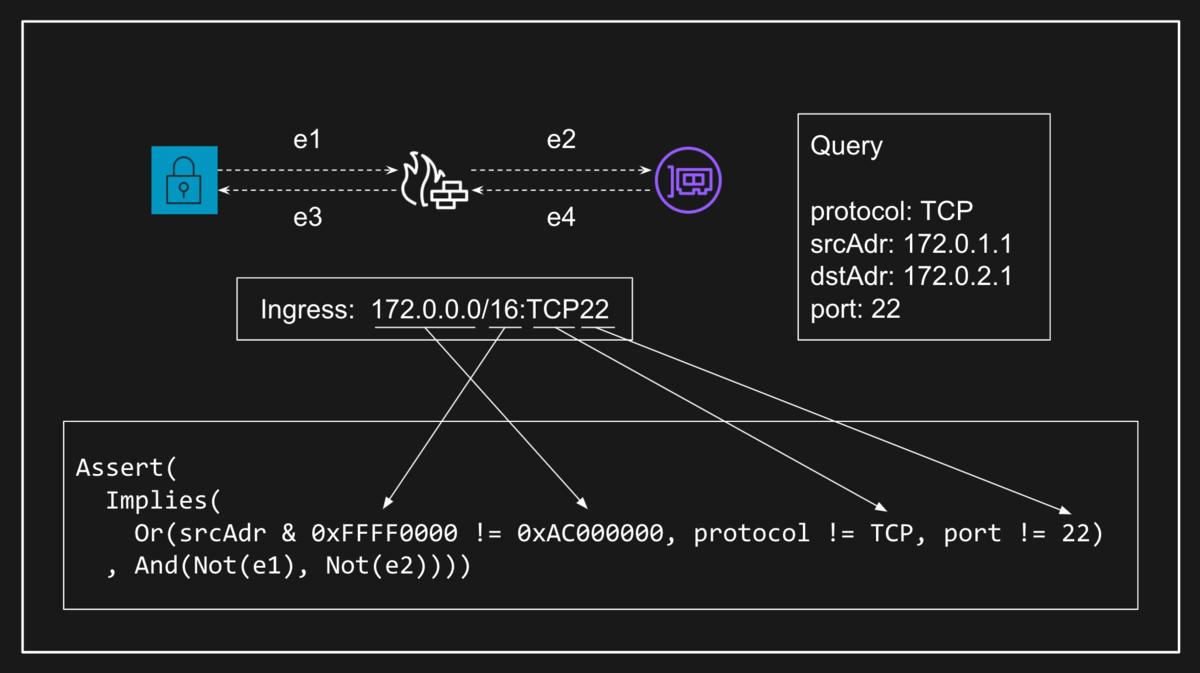
Tiros が MonoSAT を用いて VPC ネットワークの意味論を検査するさいには、MonoSAT が持っているグラフ理論用の理論ソルバを使用します。具体的には EC2 インスタンスや ENI、セキュリティグループなどのコンポーネントをノードとし、ENI とセキュリティブループ間のようなアタッチ関係をエッジとします。このとき、やはり MonoSAT が持つビットベクトルの理論ソルバを使ってコンポーネントを通過できるパケット条件を記述することで、パケットの到達可能性はグラフの到達可能性として検査することが可能になります。

ところで、MonoSAT が持つグラフ理論の理論ソルバは、汎用の SMT ソルバとしては特殊なものです。逆に言えばなぜ MonoSAT はグラフの理論ソルバを実装しているのでしょうか？

この答えは MonoSAT の提案論文である参考文献 [Bay15] に述べられています。ここで鍵になるのはと Boolean Monotonic Theories と呼ばれる理論のクラスです。Boolean Monotonic な理論では述語や関数の引数が真偽値に限定されており、かつ述語 $p$ に対して以下の性質が成り立ちます。

$p(..., s_{i-1}, 0, s_{i+1}, ...) \rightarrow p(..., s_{i-1}, 1, s_{i+1}, ...)$

つまり、その述語がある変数を偽としたときに成立するのであれば、その変数を真に変えたときでもやはり成立する、という性質です。

今回考えているグラフの到達可能性は、この Monotonic の性質を満たす述語です。実際、あるエッジが偽（接続しない）の状態で到達可能なノード同士は、そのエッジを真（接続する）に変更したとしてもやはり到達可能です。また、MonoSAT が実装している到達性以外の述語、例えば最小スパニング木の生成などについてもこの性質が成り立ちます。

理論が Monotonic である場合、理論ソルバ側の原子命題への部分的な真偽割り当てが与えられた段階で、残りをすべて真で埋めてしまって理論ソルバで検証することが可能になります。なぜなら、そうして得られた結果が充足不可能であれば、部分的な割り当ての時点で既に充足不可能であることがわかるからです。逆に、すべて偽で埋めた状況で充足可能が確定すれば、残りの変数の真偽はどちらでも問題ないことがわかります。いわば、上下からおおざっぱな評価をしてみて情報を引き出していると言えるでしょう。これを利用して探索空間を絞るのが MonoSAT の、ひいては Tiros の戦略です。

Blocked Path の検出

これは当日のプレゼンに入れられなかった補足なのですが、今年に入ってから Tiros の機能を拡張する論文 [Bay21] が出ており、しかもこの論文は VPC Reachability Analyzer に直接関係しています。具体的には、接続できない場合に原因となっているコンポーネントを検出する方法について示した論文です。

一般には、MonoSAT で到達不可能であることが示された場合、何が原因であるかは明らかではありません。理論ソルバ側が充足不可能だった場合には矛盾が生じた式の集合を返してくるため、そこから修正すべき原因を引き出してユーザに情報を提示することになります。

ここで一筋縄でいかないのは、最終的な出力として何を残す必要があるかによってアルゴリズムが変わることです。前述の論文ではこの「到達不可能な原因」を以下の 3 種類に分類しています。

ユーザがコンポーネントの設定を変更できるもの
Local Route など、変更できないが情報としては必要なもの
検査の過程で機械的に変換された変数など、提示する意味がないもの

そして、それぞれに対して「最小の矛盾集合」を段階的に得るアルゴリズムとその正当性を示す流れが論文の骨子です。

サンプル構成

今回サンプルとして使用した EC2 インスタンス 3 個からなる構成は、以下の CloudFormation テンプレートから作成することができます。なお、このテンプレートを使用することで生じた問題には一切責任は持てません。特に、小さいとはいえ実際のインスタンスを立てること、また VPC Reachability Analyzer の実行には安くない料金（0.1 USD / 検査）がかかることに注意してください。

---
Description: 'Demo for AWS Dev Day 2021: Breakout Session G-4'
AWSTemplateFormatVersion: 2010-09-09

Mappings:
  RegionMap:
    ap-northeast-1:
      execution: ami-02892a4ea9bfa2192

Resources:
  VPC:
    Type: AWS::EC2::VPC
    Properties:
      CidrBlock: 172.0.0.0/16

  SubnetX:
    Type: AWS::EC2::Subnet
    Properties:
      VpcId: !Ref VPC
      CidrBlock: 172.0.1.0/24

  SubnetY:
    Type: AWS::EC2::Subnet
    Properties:
      VpcId: !Ref VPC
      CidrBlock: 172.0.2.0/24

  SecurityGroup1:
    Type: AWS::EC2::SecurityGroup
    Properties:
      GroupDescription: 'Allow SSH from inside of the VPC'
      VpcId: !Ref VPC
      SecurityGroupIngress:
        - CidrIp: !GetAtt VPC.CidrBlock
          IpProtocol: "tcp"
          FromPort: 22
          ToPort: 22
      SecurityGroupEgress:
        - CidrIp: 0.0.0.0/0
          IpProtocol: "-1"

  SecurityGroup2:
    Type: AWS::EC2::SecurityGroup
    Properties:
      GroupDescription: 'Deny all incomming accesses'
      VpcId: !Ref VPC
      SecurityGroupEgress:
        - CidrIp: 0.0.0.0/0
          IpProtocol: "-1"

  InstanceA:
    Type: AWS::EC2::Instance
    Properties:
      ImageId:
        Fn::FindInMap:
          - RegionMap
          - !Ref AWS::Region
          - execution
      InstanceType: 't3.nano'
      SubnetId: !Ref SubnetX
      SecurityGroupIds:
        - !Ref SecurityGroup1
      Tags:
        - Key: Name
          Value: InstanceA

  InstanceB:
    Type: AWS::EC2::Instance
    Properties:
      ImageId:
        Fn::FindInMap:
          - RegionMap
          - !Ref AWS::Region
          - execution
      InstanceType: 't3.nano'
      SubnetId: !Ref SubnetY
      SecurityGroupIds:
        - !Ref SecurityGroup1
      Tags:
        - Key: Name
          Value: InstanceB

  InstanceC:
    Type: AWS::EC2::Instance
    Properties:
      ImageId:
        Fn::FindInMap:
          - RegionMap
          - !Ref AWS::Region
          - execution
      InstanceType: 't3.nano'
      SubnetId: !Ref SubnetY
      SecurityGroupIds:
        - !Ref SecurityGroup2
      Tags:
        - Key: Name
          Value: InstanceC

  ReachablePath:
    Type: AWS::EC2::NetworkInsightsPath
    Properties:
      Source: !Ref InstanceA
      Destination: !Ref InstanceB
      DestinationPort: 22
      Protocol: tcp

  UnreachablePath:
    Type: AWS::EC2::NetworkInsightsPath
    Properties:
      Source: !Ref InstanceA
      Destination: !Ref InstanceC
      DestinationPort: 22
      Protocol: tcp

まとめ

以上、AWS の VPC ネットワークにおいて、トラブルシューティングを自動化するのに便利な機能 VPC Reachability Analyzer と、そのバックエンドである Tiros、さらにその背後にある SMT ソルバ MonoSAT の特性について解説しました。

ところで、ベンチマークのスライドで述べている通り、MonoSAT は複数の経路が存在するようなケースで性能が悪化することが知られています。これは MonoSAT に限らず、一般に SMT ソルバベースのソリューションで見られる傾向です。このような場合に極力パフォーマンスを悪化させないために、Header Space Analysis と呼ばれる手法も知られているのですが、それはまた別の話。

参考文献

[Bac19] Backes, John, Sam Bayless, Byron Cook, Catherine Dodge, Andrew Gacek, Alan J. Hu, Temesghen Kahsai, et al. 2019. “Reachability Analysis for AWS-Based Networks.” In Computer Aided Verification, 231–41. Springer International Publishing.
[Bay15] Bayless, Sam, Noah Bayless, Holger Hoos, and Alan Hu. 2015. “SAT Modulo Monotonic Theories.” Proceedings of the AAAI Conference on Artificial Intelligence 29 (1). https://ojs.aaai.org/index.php/AAAI/article/view/9755.
[Bay21] Bayless, S., J. Backes, D. DaCosta, B. F. Jones, N. Launchbury, P. Trentin, K. Jewell, S. Joshi, M. Q. Zeng, and N. Mathews. 2021. “Debugging Network Reachability with Blocked Paths.” In Computer Aided Verification, 851–62. Springer International Publishing.
[Kot18] Kotelnikov, Evgenii. 2018. “Automated Theorem Proving with Extensions of First-Order Logic.” search.proquest.com. https://search.proquest.com/openview/2407fa8ebeb24157d4348884a5d03dd5/1?pq-origsite=gscholar&cbl=18750&diss=y.
[Seb07] Sebastiani, Roberto. 2007. “Lazy Satisfiability Modulo Theories.” Journal on Satisfiability, Boolean Modeling and Computation 3 (3-4): 141–224.
[Sub19] Subotic, Pavle. 2019. “Scalable Logic Defined Static Analysis.” Doctoral, UCL (University College London). https://discovery.ucl.ac.uk/id/eprint/10067190/.