Alloy で自動定理証明っぽいやつ - チェシャ猫の消滅定理

このエントリは Theorem Prover Advent Calendar 2015 - Qiita の 23 日目です。

とは言ってみたものの、内容はいわゆる定理証明器の話ではありません。モデル検査器 Alloy を利用して古典命題論理のシークエント計算をモデル化し、証明図を自動生成させることを目標にします。

なお、以下で部分的に引用しているモデル定義の完全版は alloy_sequent.als · GitHub にアップロードしてあります。

モデル化してみる

命題論理式の実装

まず対象となる論理式を Alloy で記述します。

abstract sig Formula {}

sig Atom extends Formula {}

sig Not extends Formula {
    of : one Formula,
}

abstract sig BinaryLogicOperator extends Formula {
    left  : one Formula,
    right : one Formula,
}
sig And, Or, Imply extends BinaryLogicOperator {}

二項演算子たちを定義する際、独立に定義せず間に抽象シグネチャ BinaryLogicOperator を挟んで extends で継承しています。これは Alloy 上の関係には多相性がなく、同じ名前の関係は同じシグネチャ間にしか定義することができないためです。つまり演算子をそれぞれ個別に定義した場合、引数を指す関係名を、例えば andRight : And -> Formula のように演算子ごとにつける必要が生じてしまいます。

そこで、引数を left, right とした BinaryLogicOperator を経由することで、すべての演算子に共通して課したい制約を

fact formulaeAreAcyclic {
    all f : Formula | f not in f.^(of + right + left)
}

のように統一的に記述できるというわけです。

シークエントの実装

さて、次にシークエントの定義を記述します。

sig Sequent {
    antecedents : set Formula,
    succedents  : set Formula,
}

通常の記法で言えばシークエント $\Gamma \vdash \Delta$ の $\Gamma$ が antecedents, $\Delta$ が succedents です。

本来、これらは「論理式の列」として個数と順番を考えて保持されるべきですが、今回は古典命題論理しか考えないので個数も順番も無視して単なる集合 set として扱います。部分構造論理が好きな人は潔く諦めましょう。

推論規則の実装

シークエントができたら、推論規則も Alloy に載せましょう。

論理式の場合と同じく、もとになる抽象シグネチャを定義します。

abstract sig InferenceRule {
    premises   : some Sequent,
    conclusion : one Sequent,
}

前提 premises は最大 2 個になり得るので some で、結論 conclusion は必ず 1 個なので one で定義しておきました。

なお、公理は前提が空なる推論規則であると考えて premises を set で定義することも考えられますが、この場合、検証の際に証明図を構成する InferenceRule の数が増えてしまいます。ここでは探索空間の最適化を優先することにして、公理は始シークエント InitialSequent として別途定義することにします。

そして、InferenceRule を継承して個々の推論規則を実装します。今回のように継承先によって異なる性質が要求される場合、Alloy ではシグネチャファクトで制約を記述するのが便利です。例えば以下の規則

sig NotRight extends InferenceRule {
} {
    one premises
    some f : Formula, n : Not {
        f in premises.antecedents
        f in n.of
        n in conclusion.succedents
        premises.antecedents - f = conclusion.antecedents
        premises.succedents = conclusion.succedents - n
    }
}

は否定の導入規則

$\displaystyle \frac{A, \Gamma \vdash \Delta}{\Gamma \vdash \Delta, \lnot A}$

に対応しています。

同様にして各論理演算子に対応する規則 NotLeft, AndRight, AndLeft, OrRight, OrLeft, ImplyRight, ImplyLeft を定義しておきます。

なお、すでに述べた通りシークエントに登場するコンテクストを集合として実装しているため、構造規則が必要ない（逆に言えば表現できない）ことに留意しましょう。また cut 規則も本質的には必要ないはずなのであらかじめ外しておきます。

証明図の実装

最後に、ここまで登場した要素を積み上げて全体で一つの証明図になるよう制約を加えます。

fact noIsolatedFormulae {
    Formula in Sequent.(antecedents + succedents)
}

sig RootSequent in Sequent {
} {
    this not in InferenceRule.premises
}

sig InitialSequent in Sequent {
} {
    some antecedents & succedents
}

fact rulesFormAProofTree {
    one RootSequent
    Sequent - InferenceRule.conclusion = InitialSequent
    no r : InferenceRule | r in r.^(conclusion.~premises)
    all s : Sequent - InitialSequent | one conclusion.s
}

ここでは、シークエントの中で特殊なポジションを持つものが in 記法により定義されています。証明されるべき最終的な主張が RootSequent, また公理として扱われる始シーケント

$\displaystyle A, \Gamma \vdash \Delta, A$

が InitialSequent です (2015/12/23 誤植を修正)。

証明図全体は制約 rulesFormAProofTree により、RouteSequent を根とし、InitialSequent を葉とする二分木になります。

検証してみる

無矛盾性の検証

まず、ここまでに定義した Alloy モデルを使って、矛盾を表す前件、後件ともに空なるシークエントが証明されない（であろう）ことを確認してみましょう。

assert consistency {
    no s : Sequent | s.antecedents = none && s.succedents = none
}
check consistency for 3

assert に対して check を実行すると、Alloy はアサーションに対する反例を探索します。シークエント計算が正しくモデル化されていれば、ここでは反例が発見されないはずです。

排中律の検証

もう一つ、今度は簡単な定理の例として排中律の証明を Alloy に探索させてみましょう。求めるべき主張は $\vdash A \lor \lnot A$ なので以下の pred を満たす証明図を run で探索させれば OK です。

pred excludedMiddle {
    some x : Atom, n : Not, o : Or {
        x in o.left
        n in o.right
        x in n.of
        RootSequent.antecedents = none 
        RootSequent.succedents = o
    }
}
run excludedMiddle for 3

以下のような結果が出力されます。

f:id:y_taka_23:20151223185313p:plain

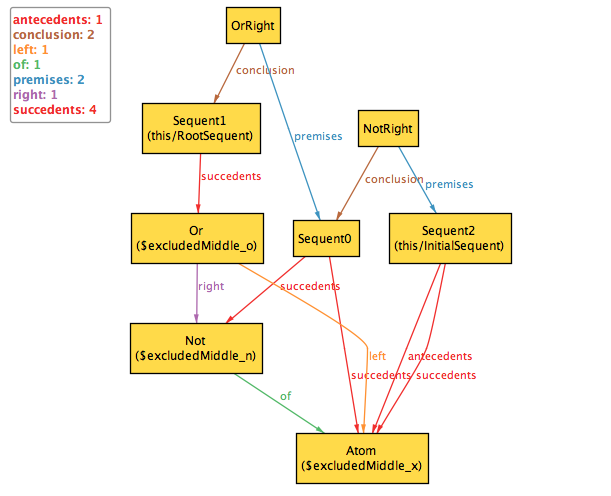
まとめ

とりあえず、今回は試みとして最も単純な古典命題論理のシークエント計算を Alloy でモデル化し、証明を自動探索させてみました。

この他にも例えば、真偽値をシグネチャとして用意し、論理式の評価結果を制約として加えれば、シークエント計算の健全性を示すことができるかもしれません。また、他の体系、例えば直観主義に変更すれば、上で示した排中律の証明は発見できなくなったりするはずです。次なる拡張の方向性はいくつかありそうですが、それはまた別の話。